2018-NIPS-[GCE]Generalized Cross Entropy Loss for Training Deep Neural Networks with Noisy Labels

https://proceedings.neurips.cc/paper_files/paper/2018/file/f2925f97bc13ad2852a7a551802feea0-Paper.pdf

Introduction

📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks. では、MAEはNoise torelantであるとわかったが、これ自体を学習に使うのはDNNにおいて向いてない。

そこで、MAEとCCEの両方を組み合わせることで、新たな損失関数GCEを開発してよい性能を得た。提案手法は以下の２つのNoisy Labelの問題設定で有効。

Open Set　訓練データの一部のNoisy Labelの本来のクラスは、与えられたクラスに含まれていないものである。
- 例えば「犬」、「猫」、「猿」のクラスがあるのに、クジラの画像とか。
Closed Set　訓練データの一部のNoisy Labelの本来のクラスは、与えられたクラスに含まれているものである。
- 「犬」を「猫」に間違えたような。

📄2020-Survey-A Survey of Label-noise Representation Learning: Past, Present and Future

ノイズ混同行列の方法については、DNNが十分な容量を持ち、ノイズ混同行列は対角優位なら、元のCCEと同じように収束するらしい。

SVMでは、Ramp, Hinge, Savage( $1/(1+\exp(y f(x)))^2$ ) Lossがノイズに強いらしい。

あとはSmall Loss Trickを使ったり、真のラベルを潜在変数として扱い、EMアルゴリズムのように解くことができる。Cleanなデータセットのgradientと近いようなサンプルはCleanだと扱うやり方もある。

Generalized Cross Entropy Loss

問題設定

サンプルは $\mathbf{x} \in X \subseteq \mathbb{R}^d$ で、ラベルは $y \in \{1, \cdots, c \}$ となる。
データは $n$ 個ある。
識別器はDNNであり、 $f(\mathbf{x}) : X \to \mathbb{R}^c$ である。
目標は次の損失関数の最小化である。

R_L(f) = \mathbb{E}[L(f(\mathbf{x}), y)]

📄2017-AAAIAI-Robust Loss Functions under Label Noise for Deep Neural Networks. によれば、MAEは対称的な損失で、次のように計算できるのでノイズに強い。

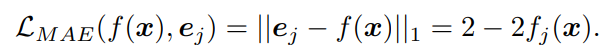
DNNではなぜMAEは悪いのか

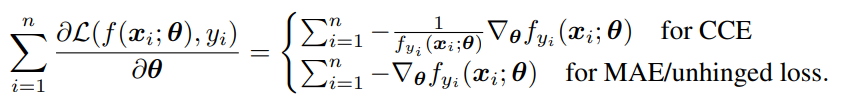
以上がCCEとMAEの勾配である。

CCEでは、 $f_{y_i}(\mathbf{x}_i;\theta)$ は予測分布の正解ラベル $y_i$ にあたる値だが、これが小さいほどがっつり学習しないといけないということで大きな重みを与えているとわかる。

Cleanなラベルでは学習を加速させるだけだが、Noisyなデータについては間違ったまま過学習させてしまう。

MAEでは、スケーリングが存在しないのでノイズには強いが学習が非常に遅く、誤ったサンプルを重点的に学習させることもまた難しい。

この問題はデータセットが難しければ難しいほど顕著になる。

提案手法

MAEの性質を保ちつつ学習が遅い問題を解決するために、Box-Cox変換をする。 $q \in (0, 1]$ 。

この時、 $q \to 0$ にしたときにロピタルの定理を使いつつ、マクローリン展開で $a^q = e^{q \log a} \approx 1 + q \log a$ を使うと、以下のようにCCEになるとわかる。

\frac{1 - f_j(\mathbf{x})^q}{q} \to \frac{- \log f_j (\mathbf{x})}{1}

Box-Cox変換した形は、以下の式のように範囲が制約されている。

最大値は、 $\sum_j f_j(x) =1$ であることから、q乗がついても $c-1$ が分子で抑えられる。

最小値は、すべての $f_j(x) = 1/c$ であるとき。

\frac{c - c(1 - q))}{q} = c \leq \sum_{j=1}^c \frac{1 - f_j(x)^q}{q} \leq \frac{c - 1}{q}

そしてこのBox-Cox変換された損失は、、先行研究のように $\eta \leq 1 - 1/c$ を満たすようなノイズがあるとき、真のラベルでの損失とNoisy Labelでの学習した損失の差は抑えられる。

$\hat{f}$ がNoisy Labelでの学習結果。

A \leq R_{L_q}(f^*) - R_{L_q}(\hat{f}) \leq 0 \\ A = \frac{\eta [1 - c(1 - q)]}{q (c - 1 - \eta c)} < 0

$q$ が1に近いほど、 $A$ は0へと近づいてよい評価になる。
$q=1$ の時はMAE損失である。
$q \to 0$ になったらCCEである。
うまく $q$ を操作することでいいとこどりの性能を得るのがGCE。

実際、GCE $L_q$ の勾配を見てみると、適切な重みをつけているように見える。

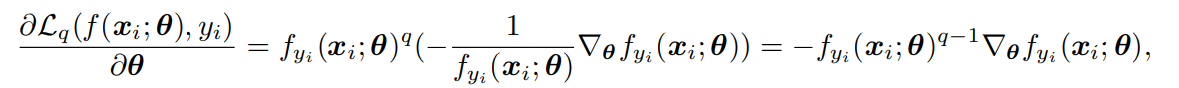
$L_q$ を切り詰める

$L_q$ をもとに新たな「切り詰めた」損失関数を定義する。

ある閾値 $k$ 以上の時はBox-Cox変換された損失関数 $L_q$ を使うが、 $k$ 未満の時は $f_j(\mathbf{x})$ の代わりに $k$ を使う、つまり $L_q(k) = (1 - k^q)/q$ となり、本来よりも損失を小さくすることができる=学習するべき影響を抑えられる。これで、Denoise機能をさらに上げることができる。

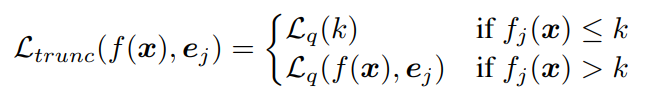
これを $v_i=0, 1$ によってどっちを使うかを選択するように定式化させると以下のようになる。

本来 $v_i$ は二値のみ取るが、これを二変数の凸最適化問題に帰着することができる。これは片方を固定してもう片方を最適化、というのを繰り返すことで最適化できる。

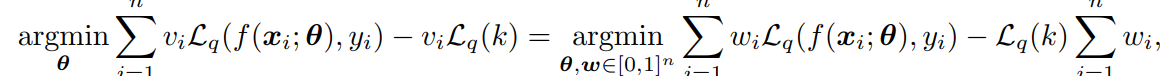
しかし、DNNは非凸関数であるものの、これと同じようにACSをしてもうまくいくことが多い。この作業をPruningという。

ACSを用いるときの最終的なアルゴリズム

すべてのパラメタにおいて、先ほどの言うようにACSを使って、相互にパラメタを更新する感じである。

もちろん、 $L_q$ だけ使ってもよい。

Experiments

$q$ が高いと、過学習が遅れてより多くの特徴を学べる。ただ多ければ多いほどいいわけじゃない。

CIFAR10, CIFAR100, FMNISTで訓練していて、 $q=0.7$ とした。